Projects
Parasol Lab
The Parasol Laboratory is a focal point for research related to next-generation computing languages and systems and for the development of algorithms and applications that exploit these to solve computation and/or data intensive applications. For more information, go to the Parasol Lab website.
Tools/APIs: ROS2, Gazebo, OpenCV

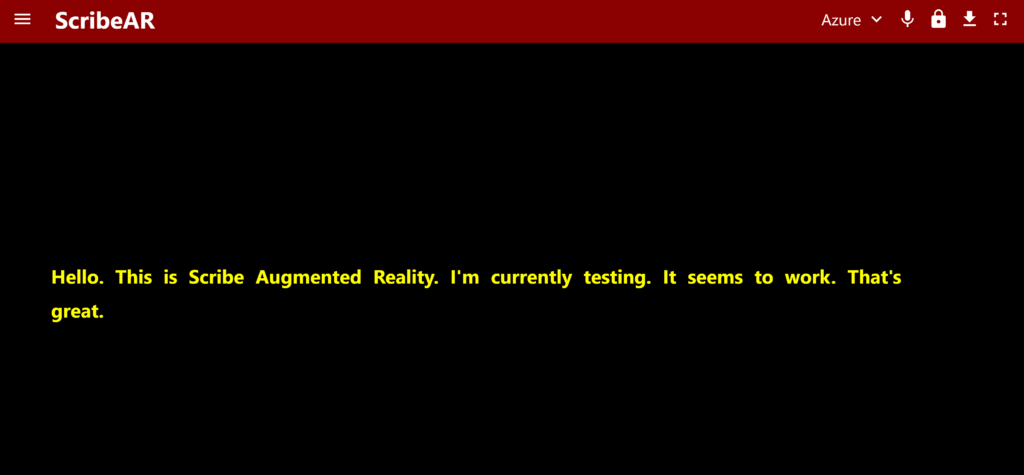
ScribeAR
ScribeAR is a lightweight web application designed for use with Augmented Reality (AR) headsets, primarily focused on providing real-time captioning for individuals who are Deaf or Hard of Hearing such that they could also equally learn in a classroom environment just like any other regular student.
Tools/APIs: React TypeScript, Material UI, Web Speech API, Microsoft Azure, Whisper CPP
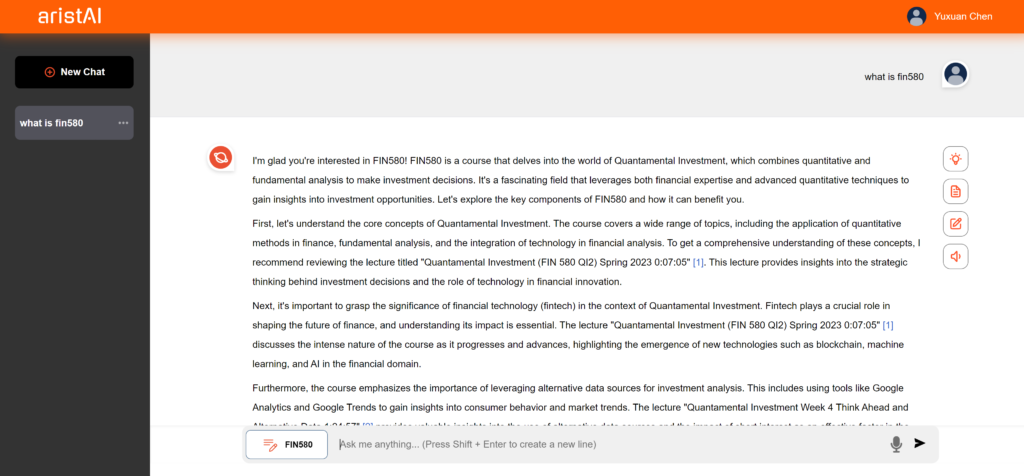
AristAI
AristAI is an AI-driven Teaching Assistant chatbot designed to generate more accurate solutions to a course while providing students with a better learning experience.
Tools: NextJS TypeScript, Tailwind CSS, Python Django, AWS
US Pollution Atlas
Using the US Pollution Dataset from Kaggle (https://www.kaggle.com/datasets/sogun3/uspollution), we have implemented a “US Pollution Atlas” that provides easy-to-use frontend toggles, CRUD operations, advanced queries of specific data, and visualizations of pollutant states.
Tools: React JavaScript, ExpressJS, MySQL, Google Cloud Platform

Ukraine OSM Data Analysis
This project investigates how the Russian Invasion of Ukraine is manifested using Open Street Map (OSM). The project centers around data and visualization of changes to OSM in various engagements.
Tools: Python, MongoDB, OSM API
Quantum Information Theory Research
In this project, we evaluate the upper bound on the quantum capacity of two quantum channels using semi-definite programming. We present data investigating the bounds and simplify our approach to linear programming.
Tools: Python
Detecting Knottedness with Quantum Computers
In this project, we show that computing the Khovanov homology of a knot diagram K in a bigrading (i, j) is in Quantum Merlin-Arthur (QMA) if the spectral gap of a certain “Laplacian” operator can be bounded by an inverse polynomial in the size of K. Motivated by the desire to understand the feasiblity of this, we present data investigating the spectral gap.
Tools: Python, Pari/GP, Ubuntu
